1 Problems handled

This is a c++ MPI/OpenMP library for solving d-dimensional Hamilton-Jacobi-Bellman equations by finite difference methods, or semi-lagrangian methods [2]. First order and second order HJ equations time-dependent or steady equations can be solved. For optimal control applications, some algorithms of optimal trajectory reconstruction are also implemented in this library.

1.1 Time-dependent equations

The problem is to find u = u(t,x) solution of

where g_border, λ(x) and u₀ are given functions, and Ω is a box of ℝ^d:

Instead of (1b), it is possible to consider other type of boundary conditions:

for a given vector π ∈ℝ^d, or

or

It is also possible to consider a combination of different types of boundary conditions: one can choose one of the above type of boundary condition, and force periodic boundary conditions on some given directions.

The function H : [0,T] × Ω ×ℝ^d →ℝ can be defined either by:

• an analytic expression, if such an expression is known (for example H(t,x,p) := c(t,x)∥p∥ + f(t,x) ⋅ p);

• or a Hamiltonian corresponding to a one-player control problem:

  

  or

  

  where A is a set of control values, of the form

  

  (with n_A ≥ 1), and where the dynamics f : [0,T] ×ℝ^d ×ℝ^n_A →ℝ^d and the distributed cost ℓ : [0,T] ×ℝ^d ×ℝ^n_A →ℝ are given functions (to be defined by the user);

• or a Hamiltonian function corresponding to a two-player game:

  

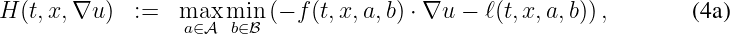
  or

  

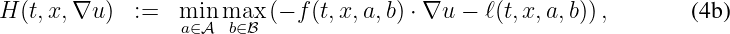
  where f, ℓ are given functions and and are control sets of the form

  

Time-dependent obstacle problem

(5)

Here H, Ω and u₀ are as above and the function g : (0,T) ×ℝ^d →ℝ is a given function. For some optimal control problems such as target problems, the set {(t,x), g(t,x) ≤ 0} may represent the set of state constraints, see [1, 3] (see also [4] as well as [5] for time-dependent state constraint and use of double obstacle problems).

Second order time-dependent equations Some second order equations can also be treated, of the following type

where is some non empty compact subset of ℝ^m (m ≥ 1) of the form

b(t,x,a) is a vector of ℝ^d, r(t,x,a) and ℓ(t,x,a) are real-valued, and σ(t,x,a) is a d × p real matrix (for some p ≥ 1). This problem is linked to the computation of the value function of stochastic optimal control problems. See section 6 for more details (a general semi-Lagrangian scheme is proposed in the software).

1.2 Steady equations

The problem is to find u = u(x) solution of an time-dependent Hamilton-Jacobi equation:

with H given directly or in the form of (3).

Obstacle problem can be also solved, of the form:

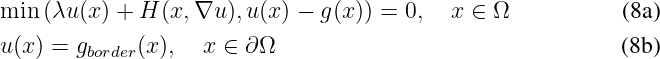
(in that case, assuming that g_border(x) ≥ g(x)).

Some second order stationary equations of the form

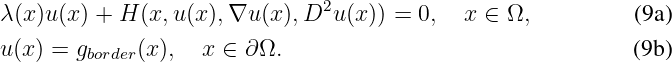
can also be solved. It is advised that the function λ(x) be strictly positive (for convergence of the solver).

The domain Ω is an hyperrectangle of ℝ^d of the form

It is possible also to solve (7a) in a subdomain . In that case the set should be defined such that

(equivalently, Ω\ = {x ∈ Ω, g_domain(x) ≥ 0}). The boundary conditions at the border of ∂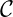 should be of Dirichlet type, fixed by the initial condition u₀(x):

This equation can be solved by using an iterative procedure - or "value iteration algorithm", where the part λ(x)u(x) is treated implicitly. Note that for steady equations (as well as time dependent equations), the basic finite difference (FD) scheme is based on the following iteration: for n ≥ 0, for a fixed Δt > 0,

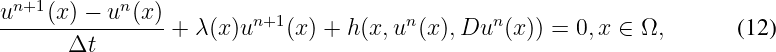
where h(x,uⁿ(x),Duⁿ(x)) corresponds to a numerical approximation of H(x,uⁿ(x),∇uⁿ(x)) and the term λ(x)u(x) is treated in an implicit way.

In the case the problem is defined only in a subdomain 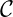as in (10), the iterations (12) are performed only at grid points x ∈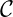. (See section 3.1 for computations in a subdomain.)

For such steady equations, once uⁿ⁺¹ has been computed, iterations are then stopped as soon as ∥uⁿ⁺¹ - uⁿ∥ _L^∞ is smaller than a given threshold. Therefore we obtain the following recursion:

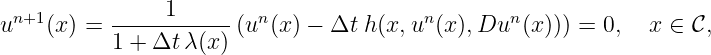
then if ∥uⁿ⁺¹ - uⁿ∥ _L^∞ ≥ ϵ go to the next step, otherwise stop. (See section 3.2.)

For the SL method, the iterative scheme is based on an implicit treatment of the λ(x)u(x) term, and becomes, in the case of (7a):

Here [uⁿ] denotes the Q ₁ interpolation of uⁿ on the spatial grid mesh.

1.3 Optimal trajectory reconstruction

In the case when the value function associated to an optimal control problem (governed by an ODE) has been solved by using for the corresponding HJB equation and by using the software, it is possible to construct also the optimal trajectory corresponding to the optimal control problem. In order to compute the optimal trajectory of the concerned problem, some reconstruction algorithms are included in the library (either based on the dynamic programming principle, or by using a minimal function assciated to the problem). In addition, the user has the possibility to implement other reconstruction methods and to test them with the software. See section 3.5 for details.