Examples

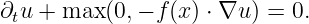
We give two ways to program an advection-like example, in files data_basicmodel.h and data_advancedmodel.h. We consider the equation

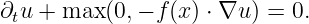
∂tu + max (0,- f (x) ⋅ ∇u ) = 0. \relax \special {t4ht=

with the parameters Ω = [-2, 2]², T = 0.5, f(x₁,x₂) = 2π(-x₂,x₁). (Hence the Hamiltonian H(x,p,t) = max(0,-f(x) ⋅ p).)

In the first way (data_basicmodel.h), we define dynamics

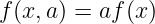
f(x,a ) = af (x) \relax \special {t4ht=

with two control values a ∈{0, 1}.

In the second way (data_advancedmodel.h), we define the Lax-Friedrich numerical hamiltonian function Hnum associated to H (see (22)).

see the files data_FD_2d_ex1_basic.h and data_FD_2d_ex1_advanced.h The problem solved is

∂tu + c(x,t)∥∇u ∥ = 0, x ∈ [- 2,2]d, t ∈ [0,T]. (20) d u(0,x ) = u0(x), x ∈ [- 2,2], (21) \relax \special {t4ht=

with d = 2, T = 1, here c(x,t) ≡ 1, and with some (radially symetric) initial data u₀(x).

In the file data_FD_2d_ex1_basic.h, a scheme is programmed using a control-discretisation of ∥∇u∥ as follows:

∥∇u ∥ ~ max ⟨(cos(θ ),sin(θ ),∇u ⟩, θ = -2kπ- k=1,...,NCD k k k NCD \relax \special {t4ht=

where NCD is the number of controls.

In the file data_FD_2d_ex1_advanced.h, a scheme is programmed using a Lax-Friedriech numerical approximation H_num associated to H :

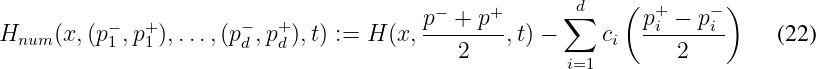
- + ∑d ( + -) H (x,(p- ,p+),...,(p-,p+ ),t) := H (x, p-+-p-,t) - c pi---pi- (22) num 1 1 d d 2 i 2 i=1 \relax \special {t4ht=

The exact solution is given for comparison.