Results on synthetic images
Letter_C
First, the method is applied on an academic example taken from [1] for
mapping a disk to the letter C, demonstrating the ability of the algorithm to
handle large deformations. Note that with linear elasticity model, diffusion model
or curvature-based model, registration cannot be successfully accomplished (see
[2]). As in [1], the right part of the disk is stretched into the shape of the interior
edge of the letter C, and then moves outward to align the interior boundary of
the letter C. Nevertheless, our deformation field is smoother (see in particular
[1, p. 88]).
 Template
Template
 Reference
Reference
 Deformed Template
Deformed Template
 Segmented Reference
Segmented Reference
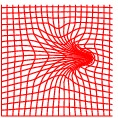 Deformation grid
Deformation grid
 Inverse Deformation grid
Inverse Deformation grid
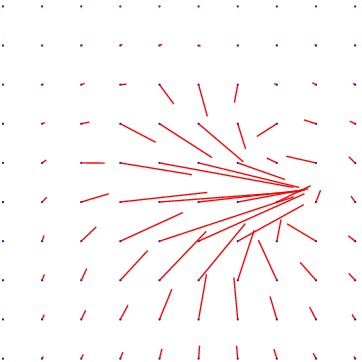 Displacement vector field
Displacement vector field
min det \(\nabla \varphi \)=0.002, max det \(\nabla \varphi \)=2.32.
\( \Delta MI = 12\% \).
Triangle
Another toy example is provided to emphasize again the capability of the model
to generate large deformations even on data corrupted by noise. The algorithm
produces both a smooth deformation field and a simplified (thus here denoised)
version of the Reference image allowing for its segmentation.
 Template
Template
 Reference
Reference
 Deformed Template
Deformed Template
 Segmented Reference
Segmented Reference
 Deformation grid
Deformation grid
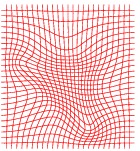 Inverse Deformation grid
Inverse Deformation grid
 Displacement vector field
Displacement vector field
min det \(\nabla \varphi \)=0.37, max det \(\nabla \varphi \)=2.25.
\( \Delta MI = 15\% \).
Results on Mouse Atlas
Then the method is applied on medical images with the goal to
map a 2D slice of mouse brain gene expression data (Template T) to its corresponding 2D slice of the mouse brain atlas, in order to facilitate the integration
of anatomic, genetic and physiologic observations from multiple subjects in a
common space. Since genetic mutations and knock-out strains of mice provide
critical models for a variety of human diseases, such linkage between genetic information and anatomical structure is important. The data are provided by the
Center for Computational Biology, UCLA. The mouse atlas acquired from the
LONI database was pre-segmented. The gene expression data were segmented
manually to facilitate data processing in other applications. Some algorithms
have been developed to automatically segment the brain area of gene expression
data. The non-brain regions have been removed to produce better matching.
Our method qualitatively performs as the one in [3] and produces a smooth
deformation field but also provides both a simplified version of the Reference
image and its segmentation.
Atlas11
 Template
Template
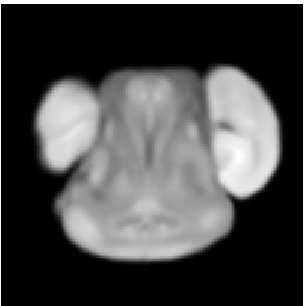 Reference
Reference
 Deformed Template
Deformed Template
 Segmented Reference
Segmented Reference
 Deformation grid
Deformation grid
 Inverse deformation
Inverse deformation
 Displacement vector field
Displacement vector field
 \(\tilde{T}\)
\(\tilde{T}\)
min det \(\nabla \varphi \)=0.63, max det \(\nabla \varphi \)=1.28.
\( \Delta MI = 6\% \).
Atlas12
 Template
Template
 Reference
Reference
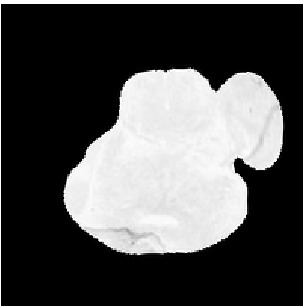 Deformed Template
Deformed Template
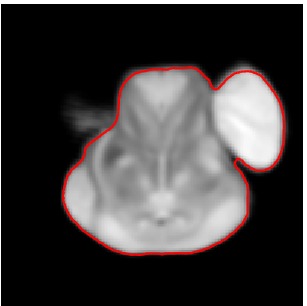 Segmented Reference
Segmented Reference
 Deformation grid
Deformation grid
 Inverse deformation
Inverse deformation
 Displacement vector field
Displacement vector field
 Ttilde
Ttilde
min det \(\nabla \varphi \)=0.68, max det \(\nabla \varphi \)=1.42.
\( \Delta MI = 14\% \).
Atlas06
 Template
Template
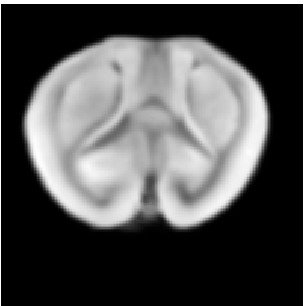 Reference
Reference
 Deformed Template
Deformed Template
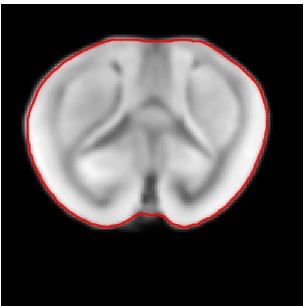 Segmented Reference
Segmented Reference
 Deformation grid
Deformation grid
 Inverse deformation
Inverse deformation
 Displacement vector field
Displacement vector field
 Ttilde
Ttilde
min det \(\nabla \varphi \)=0.46, max det \(\nabla \varphi \)=1.58.
\( \Delta MI = 35\% \).
Atlas07
 Template
Template
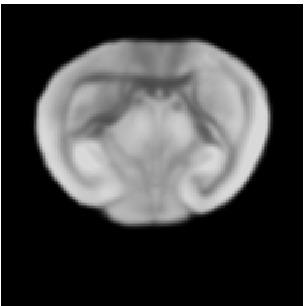 Reference
Reference
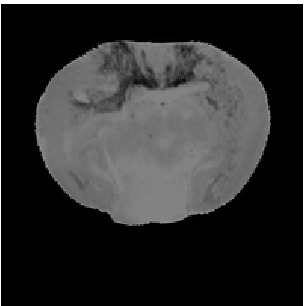 Deformed Template
Deformed Template
 Segmented Reference
Segmented Reference
 Deformation grid
Deformation grid
 Inverse deformation
Inverse deformation
 Displacement vector field
Displacement vector field
 Ttilde
Ttilde
min det \(\nabla \varphi \)=0.17, max det \(\nabla \varphi \)=1.45.
\( \Delta MI = 24\% \).
Atlas08
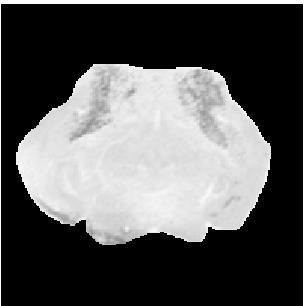 Template
Template
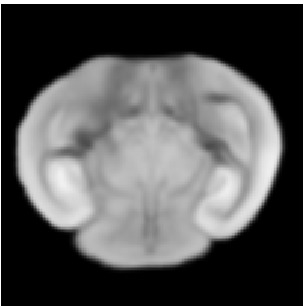 Reference
Reference
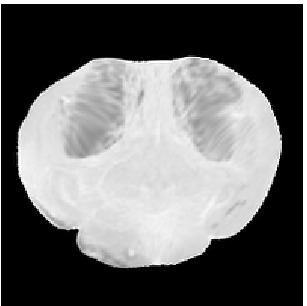 Deformed Template
Deformed Template
 Segmented Reference
Segmented Reference
 Deformation grid
Deformation grid
 Inverse deformation
Inverse deformation
 Displacement vector field
Displacement vector field
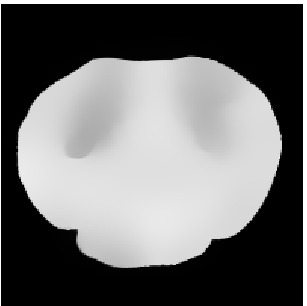 Ttilde
Ttilde
min det \(\nabla \varphi \)=0.052, max det \(\nabla \varphi \)=2.31.
\( \Delta MI = 41\% \).
Brain
The method has also been applied to complex slices of brain data (courtesy of Laboratory Of Neuro-Imaging, UCLA). We aim to register a torus to
the slice of brain with topology preservation to demonstrate the ability of the
algorithm to handle complex topologies. The results are very satisfactory on this
example since the deformed Template matches very well the convolutions of the
brain. The interior contour of the right part of the torus moves to the upper
boundary of the hole, while the exterior contour moves towards the upper envelope, entailing large deformations since the thickness of this part of the brain is
much greater than the thickness of the torus.
 Template
Template
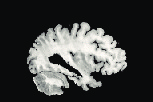 Reference
Reference
 Deformed Template
Deformed Template
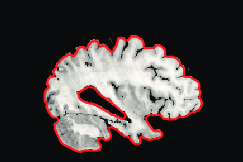 Segmented Reference
Segmented Reference
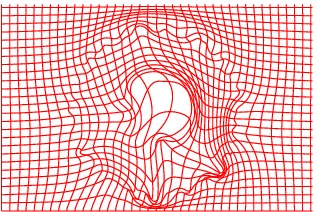 Deformation grid
Deformation grid
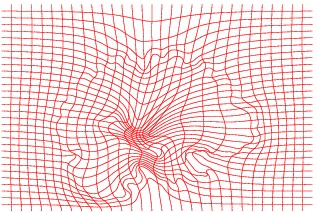 Inverse deformation
Inverse deformation
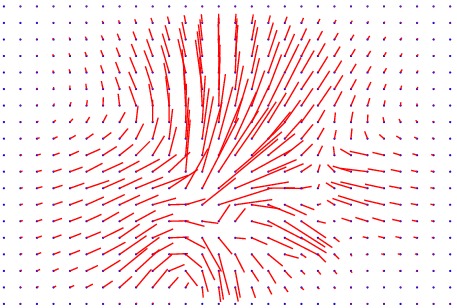 Displacement vector field
Displacement vector field
 \(\tilde{T}\)
\(\tilde{T}\)
min det \(\nabla \varphi \)=0.006, max det \(\nabla \varphi \)=14.8.
\( \Delta MI = 50\% \).
MRI images of cardiac cycle
Finally, numerical simulations on MRI images of a patient cardiac cycle have
been carried out. We were supplied with a whole cardiac MRI examination of
a patient (courtesy of the LITIS, University of Rouen, France). It is made of
280 images divided into 14 levels of slice and 20 images per cardiac cycle. The
numbering of the images goes from 0 to 279, and includes both the slice number
and the time index. The image 0 is set at the upper part of the heart and the
sequence from image 0 to image 19 contains the whole cardiac cycle for this
slice. The sequence from images 20 to 39 contains the whole cardiac cycle for
the slice underneath the previous one and so on. A cardiac cycle is composed
of a contraction phase (40% of the cycle duration), followed by a dilation phase
(60% of the cycle duration). The first image of the sequence (frames 0, 20, 40,
etc.) is when the heart is most dilated (end diastole - ED) and the 8 th of the
sequence (end systole - ES) is when the heart is most contracted. It thus seemed
relevant, in order to assess the accuracy of the proposed algorithm in handling
large deformations, to register the pair ED-ES. Besides, due to the patient’s
breathing, images from a slice to another are not stackable (whereas they should
be) so we also registered pairs of the form 120-140.
Heart ED-ES (images 80 to 88)
 Template
Template
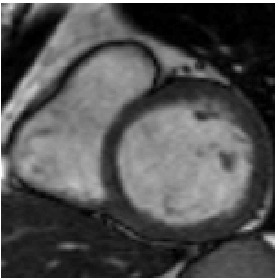 Reference
Reference
 Deformed Template
Deformed Template
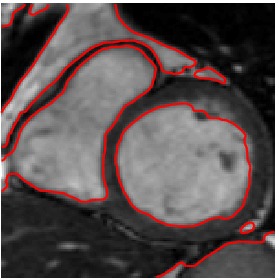 Segmented Reference
Segmented Reference
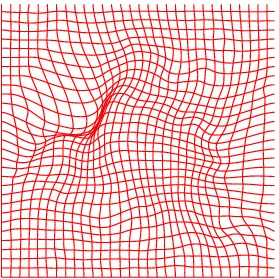 Deformation grid
Deformation grid
 Inverse deformation
Inverse deformation
 Displacement vector field
Displacement vector field
 \(\tilde{T}\)
\(\tilde{T}\)
min det \(\nabla \varphi \)=0.01, max det \(\nabla \varphi \)=3.83.
\( \Delta MI = 33\% \).
Heart ED-ES (images 100 to 108)
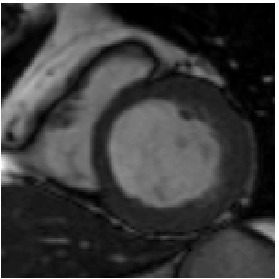 Template
Template
 Reference
Reference
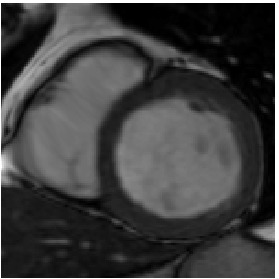 Deformed Template
Deformed Template
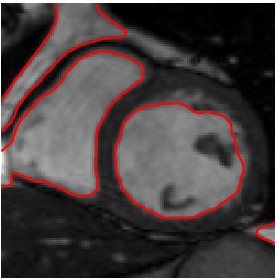 Segmented Reference
Segmented Reference
 Deformation grid
Deformation grid
 Inverse deformation
Inverse deformation
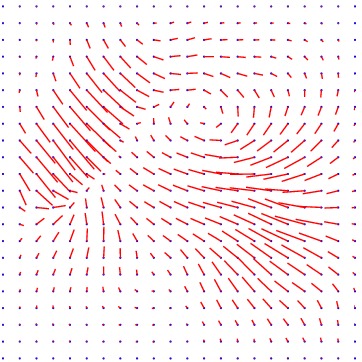 Displacement vector field
Displacement vector field
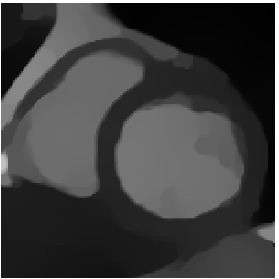 \(\tilde{T}\)
\(\tilde{T}\)
min det \(\nabla \varphi \)=0.005, max det \(\nabla \varphi \)=2.31.
\( \Delta MI =27\% \).
Heart 120-140
 Template
Template
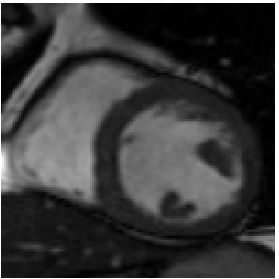 Reference
Reference
 Deformed Template
Deformed Template
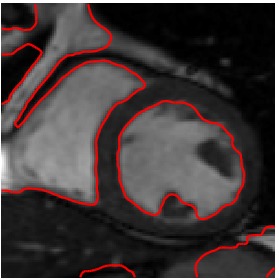 Segmented Reference
Segmented Reference
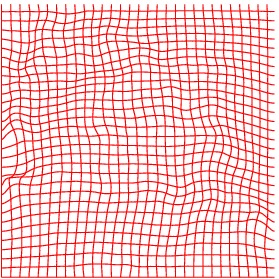 Deformation grid
Deformation grid
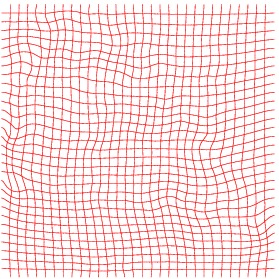 Inverse deformation
Inverse deformation
 Displacement vector field
Displacement vector field
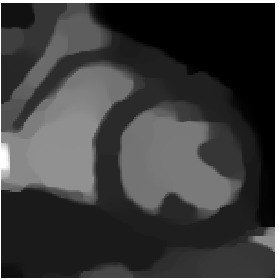 \(\tilde{T}\)
\(\tilde{T}\)
min det \(\nabla \varphi \)=0.18, max det \(\nabla \varphi \)=2.92.
\( \Delta MI = 27\% \).
Heart 160-180
 Template
Template
 Reference
Reference
 Deformed Template
Deformed Template
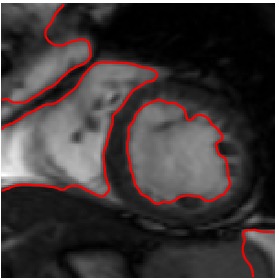 Segmented Reference
Segmented Reference
 Deformation grid
Deformation grid
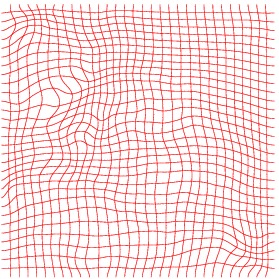 Inverse deformation
Inverse deformation
 Displacement vector field
Displacement vector field
 \(\tilde{T}\)
\(\tilde{T}\)
min det \(\nabla \varphi \)=0.11, max det \(\nabla \varphi \)=3.06.
\( \Delta MI = 24\% \).
Heart 80-81
We also have tried to register two consecutive images, however, the deformation being very small, it is quite difficult to appreciate the result.
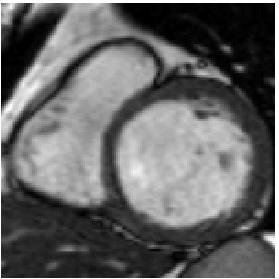 Template
Template
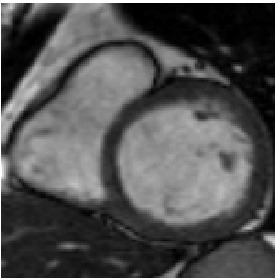 Reference
Reference
 Deformed Template
Deformed Template
 Segmented Reference
Segmented Reference
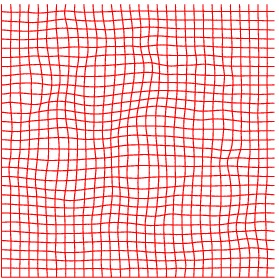 Deformation grid
Deformation grid
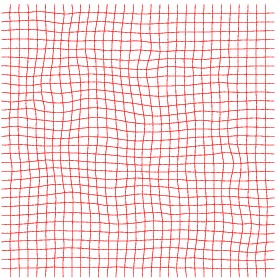 Inverse deformation
Inverse deformation
 Displacement vector field
Displacement vector field
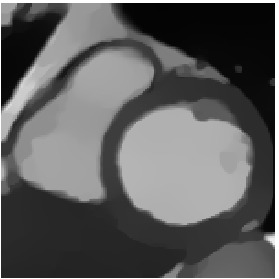 \(\tilde{T}\)
\(\tilde{T}\)
min det \(\nabla \varphi \)=0.65, max det \(\nabla \varphi \)=1.89.
\( \Delta MI = 12\% \).
Comparison with prior related works
In [3], Lin et al. first review the most common and simplest regularization terms (diffusion, biharmonic, linear elasticity models) that
lead to linear terms with respect to derivatives in the Euler-Lagrange equations. One of their conclusions is
that the biharmonic model is more comparable to the nonlinear elasticity model,
which motivates us to further examine its behaviour compared with our model.
First, we have compared the obtained results on the torus-brain example by replacing the nonlinear-elasticity-based regularizer by the biharmonic
one and by removing the weighted total variation in order to assess its relevance. The obtained deformed Template exhibits artefacts on
the boundary of the brain slice, and the hole is not satisfactorily reproduced after 40000 iterations for this algorithm versus 100 iterations for our model.
 Deformed Template
Deformed Template
The result is better adding the weighted total variation in particular on the boundary, but the hole is not reproduced either.
 Deformed Template
Deformed Template
References
- G. E. Christensen, Deformable shape models for anatomy, PhD thesis, Washing-
ton University, Sever Institute of technology, USA, 1994.
- J. Modersitzki, Numerical Methods for Image Registration, Oxford University
Press, 2004
- T. Lin, C. Le Guyader, I. Dinov, P. Thompson, A. Toga, and L. Vese,
Gene Expression Data to Mouse Atlas Registration Using a Nonlinear Elasticity
Smoother and Landmark Points Constraints, Washington, J. Sci. Comput. 50 (2012), pp. 586–
609.


 Template
Template Reference
Reference Deformed Template
Deformed Template Segmented Reference
Segmented Reference Deformation grid
Deformation grid Inverse Deformation grid
Inverse Deformation grid Displacement vector field
Displacement vector field Template
Template Reference
Reference Deformed Template
Deformed Template Segmented Reference
Segmented Reference Deformation grid
Deformation grid Inverse Deformation grid
Inverse Deformation grid Displacement vector field
Displacement vector field Template
Template Reference
Reference Deformed Template
Deformed Template Segmented Reference
Segmented Reference Deformation grid
Deformation grid Inverse deformation
Inverse deformation Displacement vector field
Displacement vector field \(\tilde{T}\)
\(\tilde{T}\) Template
Template Reference
Reference Deformed Template
Deformed Template Segmented Reference
Segmented Reference Deformation grid
Deformation grid Inverse deformation
Inverse deformation Displacement vector field
Displacement vector field Ttilde
Ttilde Template
Template Reference
Reference Deformed Template
Deformed Template Segmented Reference
Segmented Reference Deformation grid
Deformation grid Inverse deformation
Inverse deformation Displacement vector field
Displacement vector field Ttilde
Ttilde Template
Template Reference
Reference Deformed Template
Deformed Template Segmented Reference
Segmented Reference Deformation grid
Deformation grid Inverse deformation
Inverse deformation Displacement vector field
Displacement vector field Ttilde
Ttilde Template
Template Reference
Reference Deformed Template
Deformed Template Segmented Reference
Segmented Reference Deformation grid
Deformation grid Inverse deformation
Inverse deformation Displacement vector field
Displacement vector field Ttilde
Ttilde Template
Template Reference
Reference Deformed Template
Deformed Template Segmented Reference
Segmented Reference Deformation grid
Deformation grid Inverse deformation
Inverse deformation Displacement vector field
Displacement vector field \(\tilde{T}\)
\(\tilde{T}\) Template
Template Reference
Reference Deformed Template
Deformed Template Segmented Reference
Segmented Reference Deformation grid
Deformation grid Inverse deformation
Inverse deformation Displacement vector field
Displacement vector field \(\tilde{T}\)
\(\tilde{T}\) Template
Template Reference
Reference Deformed Template
Deformed Template Segmented Reference
Segmented Reference Deformation grid
Deformation grid Inverse deformation
Inverse deformation Displacement vector field
Displacement vector field \(\tilde{T}\)
\(\tilde{T}\) Template
Template Reference
Reference Deformed Template
Deformed Template Segmented Reference
Segmented Reference Deformation grid
Deformation grid Inverse deformation
Inverse deformation Displacement vector field
Displacement vector field \(\tilde{T}\)
\(\tilde{T}\) Template
Template Reference
Reference Deformed Template
Deformed Template Segmented Reference
Segmented Reference Deformation grid
Deformation grid Inverse deformation
Inverse deformation Displacement vector field
Displacement vector field \(\tilde{T}\)
\(\tilde{T}\) Template
Template Reference
Reference Deformed Template
Deformed Template Segmented Reference
Segmented Reference Deformation grid
Deformation grid Inverse deformation
Inverse deformation Displacement vector field
Displacement vector field \(\tilde{T}\)
\(\tilde{T}\) Deformed Template
Deformed Template Deformed Template
Deformed Template